Playing with Variance
Let's discuss a situation familiar to many high school students. You're taking a cutoff test like the AMC, and need at least 100 points to advance to the next round. 6 points are awarded for a correct multiple choice answer (options are A through E), 1.5 for a question left blank, and 0 for an incorrect answer. Accordingly, in isolation, it only makes sense to guess if you can eliminate at least one answer.
As an exceedingly mediocre competitive mathematician, I often found myself in the following situation: out of 25 questions, I'm sure I've answered 13 correctly. If I leave the other 12 blank, I'm certain I'll have a total of 96 points, and a 0% chance to make the cutoff. If I answer 13 correctly, leave 11 blank, and guess on 1, I'll have 94.5 points before my guess. 80% of the time, I'll guess wrong, gain zero points, and miss the cutoff. 20% of the time, I'll guess correctly, netting an extra 6 points for a total score of 100.5, and passing!
Although guessing on one question decreases my average score (from 96 to 95.7), it increases my chance of passing (from 0% to 20%)!
Here's how it looks for guessing any other number of questions:
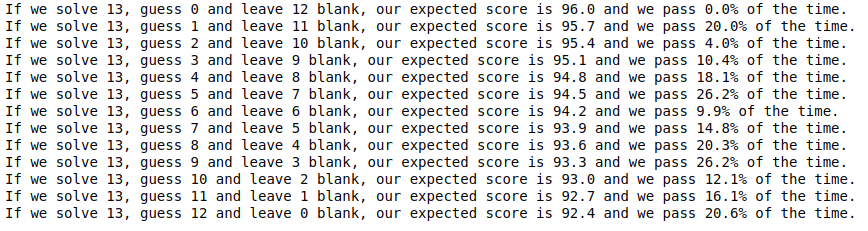
Notice that although our expected score decreases by .3 for each question we guess, our success percentage spikes at 5 and 9 guesses. We have a better chance of passing with an average score of 92.4 and very high variance than with an average score of 95.7 and low variance! Already, we've disproven the seemingly basic intuition that a higher expected score always corresponds with a higher chance of passing a fixed cutoff.
The above trend is obscured by the fact that we're using a discrete variable, so let's make this easier to see. Say you're taking a test for a pass/fail class. You need a 70% to pass the class, otherwise you'll be retaking it next semester. On average, you're scoring 76% on practice exams.
You open up the exam, and the first question is "Define courage." You can either write "This." and move on (high variance, the professor might love it or think it's ridiculous), or write a nice 5 paragraph essay about the nature of courage (low variance, the professor is likely to find it "ok").
Which should you do? Here are samples from two normal variables centered at 76, with a cutoff drawn at 70. One has high variance (standard deviation 8), and the other low variance (standard deviation 2).
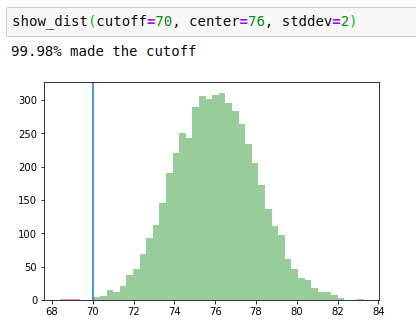
If you're expecting to pass the exam, you should pursue a low variance outcome, squishing the distribution tightly into passing grades, as seen above.
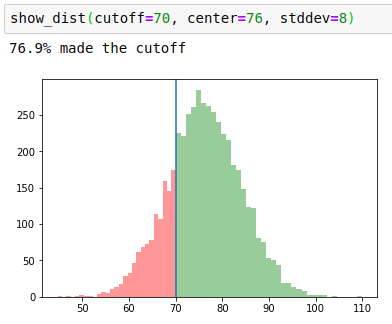
As we see in the second chart, high variance strategies will make you fail the class on your unlucky days.
Alternatively, if you were out partying until 6 in the morning and are now expecting to average a 66% on this exam, the opposite holds:
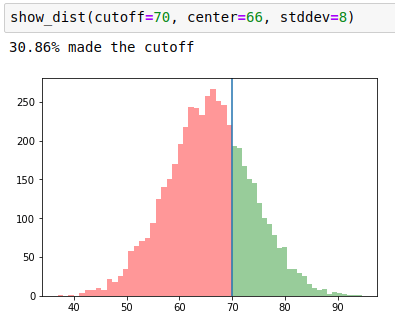
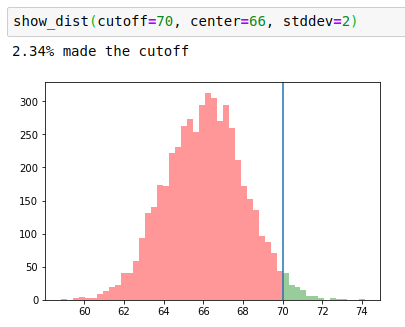
If you're expecting to fail, high variance will allow you to pass on lucky days, whereas low variance will concentrate your grades tightly around failing.
When you won't pass the cutoff on average, you want as much variance as possible. When you will pass the cutoff on average, you want as little variance as possible. This can be true even if you need to decrease your expected value to move your variance in the correct direction.
This holds in a wide range of activities. In hockey, if you're down a goal with two minutes to go, you pull your goalie to increase variance, which gives you a greater chance of winning, even if it has a negative expected value (usually, you let in more goals than you score when you pull the goalie). Alternatively, if you're up a goal with two minutes to go, play defensively (low variance strategy), even if you expect that offensive play will net you more goals on average.
If you're on a waitlist with a 0.5% admit rate, write an outrageous letter of continued interest (high variance strategy). On your lucky days, it'll allow you to get in, and on your unlucky days, it's no worse than writing a boring "I'm still interested in your school" letter (low variance strategy). If you're a triple legacy with a perfect SAT score who's cured four diseases in high school, write a bland essay (low variance strategy). You don't want to take the risk of writing an interesting essay and having it rub your admissions officer the wrong way, ruining an otherwise overwhelmingly likely decision to admit.
If you're unqualified and trying to get elected to public office in a dense field of qualified candidates, say some outrageous things (high variance strategy). If it catches on, you might win, and if it doesn't, no harm done--you weren't going to win with a low variance strategy anyway. Alternatively, if you're the most qualified candidate in a shallow field, keep your campaign within the bounds of normalcy (low variance strategy)--you'll probably win if nothing unexpected happens.
